Notice
Recent Posts
Recent Comments
Link
«   2025/01   »
일 월 화 수 목 금 토
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
Tags more
Archives
Today
Total
관리 메뉴

코딩로그

7-1. ML의 실용과 몇가지 팁 본문

코딩로그/모두를 위한 딥러닝

7-1. ML의 실용과 몇가지 팁

hyeonnny 2020. 1. 11. 13:21
  • 이번 시간에는 효율적인 ML을 위한 몇가지 팁에 대해 알아보겠다.

<Learning rate와 데이터 전처리, overfitting>

  • Learning rate : $W := W-\alpha \frac{\partial  }{\partial W}cost(W)$ 에서 알파에 해당하는 값이다. 
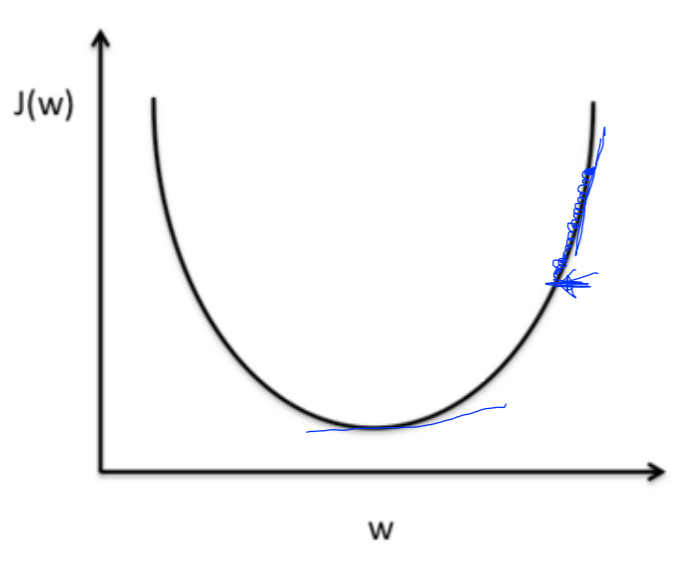
    • 너무 크면 cost의 최저값을 넘어가 버리고, 결국 주변을 맴돌다 외부로 나가버리는 overshooting 문제가 발생한다.
    • 너무 작으면 지역 최소값에 도달하거나, 시간이 너무 오래 걸리는 문제가 발생한다.
    • learning rate를 정하는데 특별한 규칙이 있는 것은 아니다. 그러나 따라서 cost function을 관찰하며 임의대로 값을 바꿔준다.

learning rate가 클 때

 

  • 데이터 전처리 : training 전 데이터를 학습하기 좋게 처리해두는 것이다.
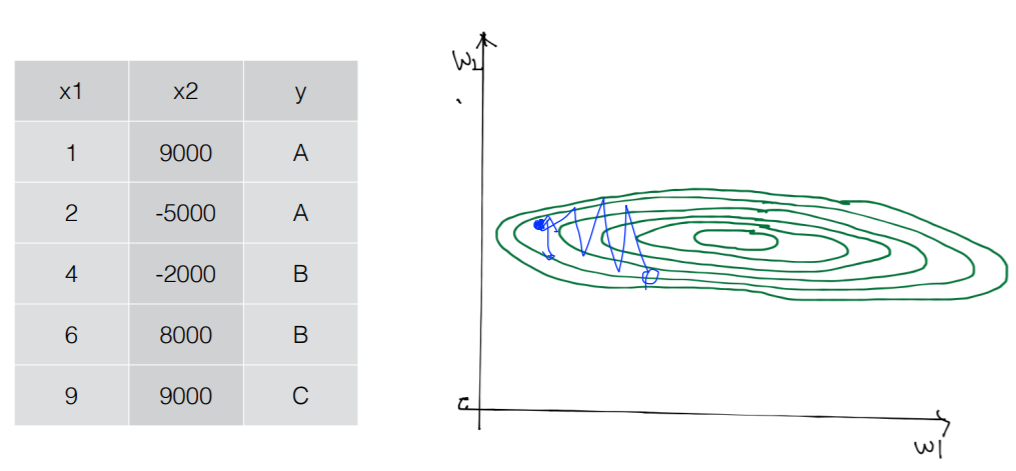
    • 그림 1과 같이 x1과 x2가 큰 차이를 보이는 데이터가 있다고 하자. 그럼 cost function은 길쭉한 형태를 띌 것이다. 이 경우 처음의 알파값이 매우 좋은 값임에도 w2축에의해 미세한 차이에도 밖으로 튀어나간다
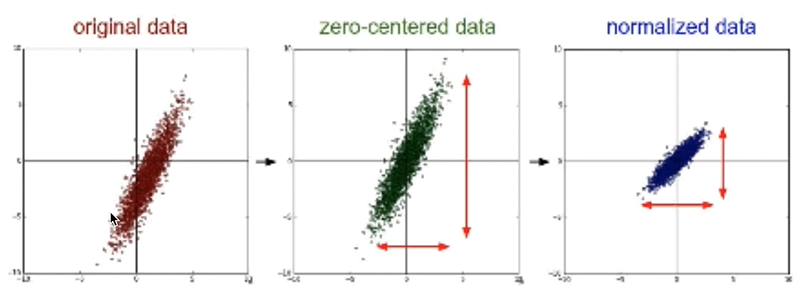
    • 따라서 데이터의 중심이 원점인 zero-center data, 가로 세로가 비슷한 normalized data로 만드는 전처리 과정을 거친다.
    • 전처리 방법 : ${x}'_{j}=\frac{x_{j}-\mu _{j}}{\sigma _{j}}$수식을 이용하면 된다. 데이터에서 평균을 빼준 값을 분산으로 나눠주는 것이다.

그림1 - 전처리 되지 않은 데이터
그림2 - 전처리 방법

 

  • overfitting
    • overfitting: training data에 너무 맞추어져 training data에서는 잘 작동했으나, 실제 데이터에서는 잘 작동하지 않는 것
    • overfitting을 방지하는 법
      1. 더 많은 training data
      2. 특성의 개수를 줄인다.
      3. regularization
    • ragularization : overfitting된 데이터를 일반화하는 기법이다. cost function에 $\lambda \sum W^{2}$을 더한다. 여기서 람다는 regularization strength로, 얼마나 regularization할 지를 나타낸다.

<Training/Testing 데이터 셋>

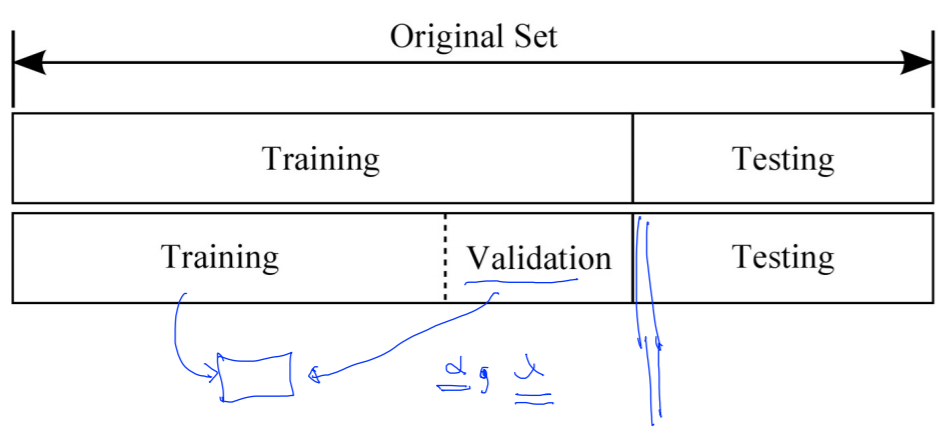
training set과 test set을 분리해 model의 성능을 테스트 할 수 있다. 또, validation data set을 만들어 learning rate나 regularization strength 등을 조정할 수 있다.

 

<실습1 - learning rate에 따른 학습효율>

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import numpy as np
 
x_data = [[1, 2, 1],
          [1, 3, 2],
          [1, 3, 4],
          [1, 5, 5],
          [1, 7, 5],
          [1, 2, 5],
          [1, 6, 6],
          [1, 7, 7]]
y_data = [[0, 0, 1],
          [0, 0, 1],
          [0, 0, 1],
          [0, 1, 0],
          [0, 1, 0],
          [0, 1, 0],
          [1, 0, 0],
          [1, 0, 0]]
 
# Evaluation our model using this test dataset
x_test = [[2, 1, 1],
          [3, 1, 2],
          [3, 3, 4]]
y_test = [[0, 0, 1],
          [0, 0, 1],
          [0, 0, 1]]
 
X = tf.placeholder("float", [None, 3])
Y = tf.placeholder("float", [None, 3])
 
W = tf.Variable(tf.random_normal([3, 3]))
b = tf.Variable(tf.random_normal([3]))
 
# tf.nn.softmax computes softmax activations
# softmax = exp(logits) / reduce_sum(exp(logits), dim)
hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
 
# Cross entropy cost/loss
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
# Try to change learning_rate to small numbers
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
 
# Correct prediction Test model
prediction = tf.argmax(hypothesis, 1)
is_correct = tf.equal(prediction, tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))
 
# Launch graph
with tf.Session() as sess:
    # Initialize TensorFlow variables
    sess.run(tf.global_variables_initializer())
 
    for step in range(201):
        cost_val, W_val, _ = sess.run([cost, W, optimizer], feed_dict={X: x_data, Y: y_data})
        print(step, cost_val, W_val)
 
    # predict
    print("Prediction:", sess.run(prediction, feed_dict={X: x_test}))
    # Calculate the accuracy
    print("Accuracy: ", sess.run(accuracy, feed_dict={X: x_test, Y: y_test}))
 
'''
learning rate : 2.0
0 2.481961 [[ 0.808544   1.3013937 -1.6374297]
 [-0.5847428  1.9140662 -4.0825534]
 [ 1.1045763  2.8628712 -1.618924 ]]
1 18.824436 [[ 1.3084809   0.05145693 -0.8874297 ]
 [ 2.66513    -3.3358064  -2.0825534 ]
 [ 4.354512   -2.137064    0.13107598]]
2 nan [[nan nan nan]
 [nan nan nan]
 [nan nan nan]]
3 nan [[nan nan nan]
 [nan nan nan]
 [nan nan nan]]
...
200 nan [[nan nan nan]
 [nan nan nan]
 [nan nan nan]]
Prediction: [0 0 0]
Accuracy:  0.0
너무 클 때 : 값이 발산.
---------------------
learing rate : 1e-10
0 2.556754 [[ 0.72504026 -0.51842254  1.6360186 ]
 [ 0.47661072  0.02948774  0.3603019 ]
 [ 1.9966121   1.9674194   1.5864257 ]]
1 2.556754 [[ 0.72504026 -0.51842254  1.6360186 ]
 [ 0.47661072  0.02948774  0.3603019 ]
 [ 1.9966121   1.9674194   1.5864257 ]]
2 2.556754 [[ 0.72504026 -0.51842254  1.6360186 ]
 [ 0.47661072  0.02948774  0.3603019 ]
 [ 1.9966121   1.9674194   1.5864257 ]]
3 2.556754 [[ 0.72504026 -0.51842254  1.6360186 ]
 [ 0.47661072  0.02948774  0.3603019 ]
 [ 1.9966121   1.9674194   1.5864257 ]]
4 2.556754 [[ 0.72504026 -0.51842254  1.6360186 ]
 [ 0.47661072  0.02948774  0.3603019 ]
 [ 1.9966121   1.9674194   1.5864257 ]]
 ...
 
196 2.556754 [[ 0.72504026 -0.51842254  1.6360186 ]
 [ 0.47661072  0.02948774  0.3603019 ]
 [ 1.9966121   1.9674194   1.5864257 ]]
197 2.556754 [[ 0.72504026 -0.51842254  1.6360186 ]
 [ 0.47661072  0.02948774  0.3603019 ]
 [ 1.9966121   1.9674194   1.5864257 ]]
198 2.556754 [[ 0.72504026 -0.51842254  1.6360186 ]
 [ 0.47661072  0.02948774  0.3603019 ]
 [ 1.9966121   1.9674194   1.5864257 ]]
199 2.556754 [[ 0.72504026 -0.51842254  1.6360186 ]
 [ 0.47661072  0.02948774  0.3603019 ]
 [ 1.9966121   1.9674194   1.5864257 ]]
200 2.556754 [[ 0.72504026 -0.51842254  1.6360186 ]
 [ 0.47661072  0.02948774  0.3603019 ]
 [ 1.9966121   1.9674194   1.5864257 ]]
 Prediction: [0 2 0]
Accuracy:  0.33333334
너무 작을 때 : cost 값이 갈수록 변하지 않고 머뭄
------------------------------------------
learning rate = 0.1
0 7.816813 [[ 2.1723878   0.07433416 -1.2341454 ]
 [ 0.21955611  0.5635566   0.02322271]
 [-1.9038371   0.72041076  0.8329903 ]]
1 5.7353907 [[ 2.1945105   0.0164572  -1.1983912 ]
 [ 0.37612408  0.31218928  0.11802205]
 [-1.7443941   0.4801206   0.91383743]]
2 4.0159507 [[ 2.2119024  -0.01537871 -1.1839471 ]
 [ 0.52209353  0.17413075  0.11011114]
 [-1.5908499   0.35747302  0.88294077]]
3 3.3536198 [[ 2.2238827  -0.0203157  -1.1909903 ]
 [ 0.654227    0.16626558 -0.01415713]
 [-1.4458715   0.36146015  0.7339753 ]]
4 2.790309 [[ 2.2314658  -0.04597655 -1.1729126 ]
 [ 0.772606    0.0397604  -0.00603092]
 [-1.3106072   0.24059848  0.7195727 ]]
 ...
 199 0.67208993 [[ 0.20719977 -0.25526592  1.0606424 ]
 [ 0.39176708  0.18911055  0.22545832]
 [ 0.13889554  0.14250961 -0.6318402 ]]
200 0.67086613 [[ 0.2019619  -0.25551403  1.0661284 ]
 [ 0.3921595   0.18955901  0.22461747]
 [ 0.14058895  0.14238301 -0.63340706]]
Prediction: [2 2 2]
Accuracy:  1.0
'''
 cs

<실습2 - data 전처리와 학습효율>

  • 전처리 되지 않은 데이터
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import numpy as np
 
#전처리 되지 않은 데이터
xy = np.array([[828.659973, 833.450012, 908100, 828.349976, 831.659973],
               [823.02002, 828.070007, 1828100, 821.655029, 828.070007],
               [819.929993, 824.400024, 1438100, 818.97998, 824.159973],
               [816, 820.958984, 1008100, 815.48999, 819.23999],
               [819.359985, 823, 1188100, 818.469971, 818.97998],
               [819, 823, 1198100, 816, 820.450012],
               [811.700012, 815.25, 1098100, 809.780029, 813.669983],
               [809.51001, 816.659973, 1398100, 804.539978, 809.559998]])
 
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]
 
# placeholders for a tensor that will be always fed.
X = tf.placeholder(tf.float32, shape=[None, 4])
Y = tf.placeholder(tf.float32, shape=[None, 1])
 
W = tf.Variable(tf.random_normal([4, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
 
# Hypothesis
hypothesis = tf.matmul(X, W) + b
 
# Simplified cost/loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y))
 
# Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-5)
train = optimizer.minimize(cost)
 
# Launch the graph in a session.
sess = tf.Session()
# Initializes global variables in the graph.
sess.run(tf.global_variables_initializer())
 
for step in range(101):
    cost_val, hy_val, _ = sess.run(
        [cost, hypothesis, train], feed_dict={X: x_data, Y: y_data})
    print(step, "Cost: ", cost_val, "\nPrediction:\n", hy_val)
 
 
'''
0 Cost:  2.45533e+12
Prediction:
 [[-1104436.375]
 [-2224342.75 ]
 [-1749606.75 ]
 [-1226179.375]
 [-1445287.125]
 [-1457459.5  ]
 [-1335740.5  ]
 [-1700924.625]]
1 Cost:  2.69762e+27
Prediction:
 [[  3.66371490e+13]
 [  7.37543360e+13]
 [  5.80198785e+13]
 [  4.06716290e+13]
 [  4.79336847e+13]
 [  4.83371348e+13]
 [  4.43026590e+13]
 [  5.64060907e+13]]
2 Cost:  inf
Prediction:
 [[ -1.21438790e+21]
 [ -2.44468702e+21]
 [ -1.92314724e+21]
 [ -1.34811610e+21]
 [ -1.58882674e+21]
 [ -1.60219962e+21]
 [ -1.46847142e+21]
 [ -1.86965602e+21]]
3 Cost:  inf
Prediction:
 [[  4.02525216e+28]
 [  8.10324465e+28]
 [  6.37453079e+28]
 [  4.46851237e+28]
 [  5.26638074e+28]
 [  5.31070676e+28]
 [  4.86744608e+28]
 [  6.19722623e+28]]
4 Cost:  inf
Prediction:
 [[ -1.33422428e+36]
 [ -2.68593010e+36]
 [ -2.11292430e+36]
 [ -1.48114879e+36]
 [ -1.74561303e+36]
 [ -1.76030542e+36]
 [ -1.61338091e+36]
 [ -2.05415459e+36]]
5 Cost:  inf
Prediction:
 [[ inf]
 [ inf]
 [ inf]
 [ inf]
 [ inf]
 [ inf]
 [ inf]
 [ inf]]
6 Cost:  nan
Prediction:
 [[ nan]
 [ nan]
 [ nan]
 [ nan]
 [ nan]
 [ nan]
 [ nan]
 [ nan]]
'''
 
 cs

전

 

  • 전처리 된 데이터
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import numpy as np
 
#전처리하는 함수
def min_max_scaler(data):
    numerator = data - np.min(data, 0)
    denominator = np.max(data, 0) - np.min(data, 0)
    return numerator / (denominator + 1e-7)
 
 
xy = np.array(
    [
        [828.659973, 833.450012, 908100, 828.349976, 831.659973],
        [823.02002, 828.070007, 1828100, 821.655029, 828.070007],
        [819.929993, 824.400024, 1438100, 818.97998, 824.159973],
        [816, 820.958984, 1008100, 815.48999, 819.23999],
        [819.359985, 823, 1188100, 818.469971, 818.97998],
        [819, 823, 1198100, 816, 820.450012],
        [811.700012, 815.25, 1098100, 809.780029, 813.669983],
        [809.51001, 816.659973, 1398100, 804.539978, 809.559998],
    ]
)
 
# very important. It does not work without it.
xy = min_max_scaler(xy)
print(xy)
 
'''
[[0.99999999 0.99999999 0.         1.         1.        ]
 [0.70548491 0.70439552 1.         0.71881782 0.83755791]
 [0.54412549 0.50274824 0.57608696 0.606468   0.6606331 ]
 [0.33890353 0.31368023 0.10869565 0.45989134 0.43800918]
 [0.51436    0.42582389 0.30434783 0.58504805 0.42624401]
 [0.49556179 0.42582389 0.31521739 0.48131134 0.49276137]
 [0.11436064 0.         0.20652174 0.22007776 0.18597238]
 [0.         0.07747099 0.5326087  0.         0.        ]]
'''
 
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]
 
# placeholders for a tensor that will be always fed.
X = tf.placeholder(tf.float32, shape=[None, 4])
Y = tf.placeholder(tf.float32, shape=[None, 1])
 
W = tf.Variable(tf.random_normal([4, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
 
# Hypothesis
hypothesis = tf.matmul(X, W) + b
 
# Simplified cost/loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y))
 
# Minimize
train = tf.train.GradientDescentOptimizer(learning_rate=1e-5).minimize(cost)
 
# Launch the graph in a session.
with tf.Session() as sess:
    # Initializes global variables in the graph.
    sess.run(tf.global_variables_initializer())
 
    for step in range(101):
        _, cost_val, hy_val = sess.run(
            [train, cost, hypothesis], feed_dict={X: x_data, Y: y_data}
        )
        print(step, "Cost: ", cost_val, "\nPrediction:\n", hy_val)
 
'''
0 Cost: 0.15230925 
Prediction:
 [[ 1.6346191 ]
 [ 0.06613699]
 [ 0.3500818 ]
 [ 0.6707252 ]
 [ 0.61130744]
 [ 0.61464405]
 [ 0.23171967]
 [-0.1372836 ]]
1 Cost: 0.15230872 
Prediction:
 [[ 1.634618  ]
 [ 0.06613836]
 [ 0.35008252]
 [ 0.670725  ]
 [ 0.6113076 ]
 [ 0.6146443 ]
 [ 0.23172   ]
 [-0.13728246]]
...
99 Cost: 0.1522546 
Prediction:
 [[ 1.6345041 ]
 [ 0.06627947]
 [ 0.35014683]
 [ 0.670706  ]
 [ 0.6113161 ]
 [ 0.61466044]
 [ 0.23175153]
 [-0.13716647]]
100 Cost: 0.15225402 
Prediction:
 [[ 1.6345029 ]
 [ 0.06628093]
 [ 0.35014752]
 [ 0.67070574]
 [ 0.61131614]
 [ 0.6146606 ]
 [ 0.23175186]
 [-0.13716528]]
'''
 
 cs

 

'코딩로그 > 모두를 위한 딥러닝' 카테고리의 다른 글

8. 딥러닝의 기본 개념과, 문제, 그리고 해결  (0) 2020.01.11
7-2. ML의 실용 : mnist data set 실습  (0) 2020.01.11
6. softmax regression  (0) 2020.01.11
5. logistic classification  (0) 2020.01.10
*tip* TensorFlow로 파일에서 데이터 읽어오기  (0) 2020.01.10
'코딩로그/모두를 위한 딥러닝' Related Articles more