코딩로그
신경망과 딥러닝 - 신경망과 로지스틱 회귀 본문
- 이진 분류
- 신경망에서 학습하는 방법 : 정방향 전파, 역전파 -> 로지스틱 분류와 비교할 것
- 이진분류 : 그렇다/아니다 2개로 분류하는 것이다. 아래 사진에서는 만약 고양이가 맞다면
1로 분류하고, 고양이가 아니면 0이라고 분류한다.
- 이미지의 특성벡터로의 변환 : 특성벡터로 변환하기 위해 벡터를 쭉 펼친다.
64x64 이미지가 있을 때 RGB의 세 채널이 있으므로 64x64x3인 12288짜리 사이즈의 특성벡터로 만든다.
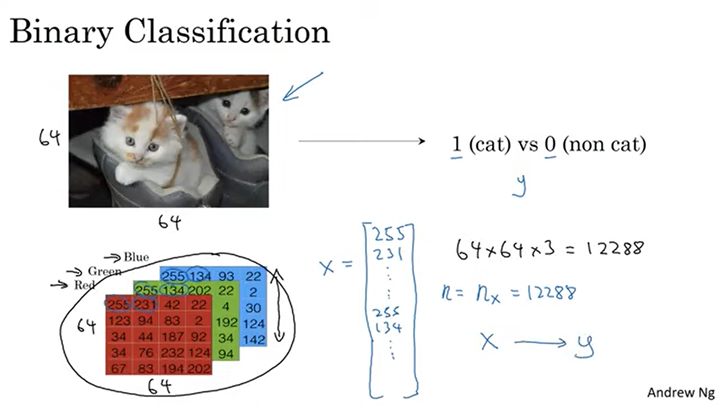
- x라는 특성벡터를 이용하여 y라는 결과를 도출해 내는 것이 로지스틱 회귀의 목적이다.
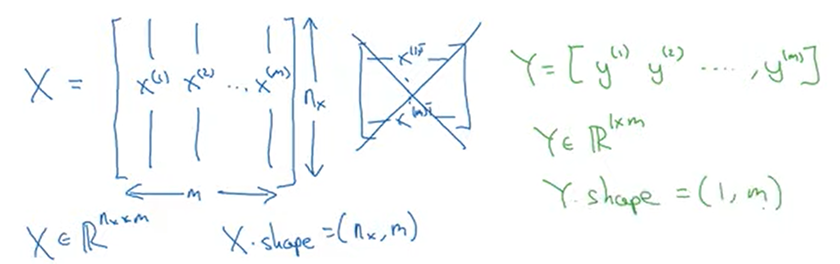
- 훈련횟수를 M이라고 하자. 그때 X와 Y를 행렬로 나타내면 다음과 같다.
- 로지스틱 회귀
- 로지스틱 회귀란 답이 0 또는 1로 정해져있는 이진 분류 문제에 사용되는 알고리즘입니다.
- X (입력 특성), y (주어진 입력특성 X에 해당하는 실제 값) y^ (y의 예측값) 을 의미합니다.
- 더 자세히 이진 분류를 위한 y^ 값은 y가 1일 확률을 의미하며 0 ≤y^≤ 1 사이의 값을 가져야 합니다.
- 선형 회귀시 y^ = WTX+b 를 통해 계산하지만, 해당 값은 0과 1 범위를 벗어날 수 있습니다. 따라서 시그모이드 함수를 통해 0과 1사이의 값으로 변환해줍니다.
- 따라서 로지스틱 회귀를 위한 y^=σ(WTX+b) 로 구하게 됩니다.
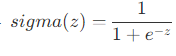

- 로지스틱 회귀의 비용함수
- 우리의 목표는 실제값(y)에 가까운 예측값( y^ )를 구하는 것입니다.
- 손실 함수는 하나의 입력특성(x)에 대한 실제값(y)과 예측값( y^ ) 의 오차를 계산하는 함수입니다.
- 보통 손실함수는 L(y^,y)=21(y^−y)2 식을 사용하지만 로지스틱 회귀에서 이러한 손실 함수를 사용하면 지역 최소값에 빠질 수 있기 때문에 사용하지 않습니다. (해당 내용은 향후 다시 나올것이니 걱정하지 않으셔도 됩니다.)
- 로지스틱 회귀에서 사용하는 손실 함수는 다음과 같습니다.
L(y^,y)=−(ylogy^+(1−y)log(1−y^))
이 함수를 직관적으로 이해하기 위해 두 가지 경우로 나누어 생각해 볼 수 있습니다.
1) y = 0 인 경우 L(y^,y)=−log(1−y^) 가 0에 가까워지도록 y^ 는 0에 수렴하게 됩니다.
2) y = 1 인 경우 L(y^,y)=−logy^ 가 0에 가까워지도록 y^ 는 1에 수렴하게 됩니다.
- 하나의 입력에 대한 오차를 계산하는 함수를 손실 함수라고 하며, 모든 입력에 대한 오차를 계산하는 함수는 비용 함수라고 합니다.
- 따라서 비용 함수는 모든 입력에 대해 계산한 손실 함수의 평균 값으로 구할 수 있으며 식으로 나타내면 다음과 같습니다.
J(w,b)=−m1Σi=1i=m(y(i)logy^(i)+(1−y(i))log(1−y^(i)))
- 경사하강법
- 이전 시간의 비용함수가 전체 데이터셋의 예측이 얼마나 잘 평가되었는지 보는 것이라면, 경사하강법은 이를 가능케하는 파라미터 w와 b를 찾아내는 방법 중 하나 입니다.
- 우선, 비용 함수는 볼록한 형태여야 합니다. 볼록하지 않은 함수를 쓰게 되면, 경사하강법을 통해 최적의 파라미터를 찾을 수 없습니다.
- 함수의 최소값을 모르기 때문에, 임의의 점을 골라서 시작합니다.
- 경사하강법은 가장 가파른(steepest) 방향, 즉 함수의 기울기를 따라서 최적의 값으로 한 스텝씩 업데이트하게 됩니다.
- 알고리즘은 아래와 같습니다.
- w:w−αdwdJ(w,b)
- b:b−αdbdJ(w,b)
- α : 학습률이라고 하며, 얼만큼의 스텝으로 나아갈 것인지 정합니다.
- dwdJ(w)
: 도함수라고 하며, 미분을 통해 구한 값 입니다. dw 라고 표기하기도 합니다.
- 만약 dw >0 이면, 파라미터 w 는 기존의 w 값 보다 작은 방향으로 업데이트 될 것이고, 만약 dw <0 이면, 파라미터 w 는 기본의 w 값 보다 큰 방향으로 업데이트 될 것입니다.
- 도함수는 함수의 기울기라고 볼 수 있습니다.
- 하나의 변수에 대한 도함수는 dw=dwdf(w) 라고 표기하지만 두 개 이상은 보통 아래와 같이 표현 합니다
- dw=∂w∂J(w,b) : 함수의 기울기가 w 방향으로 얼만큼 변했는지 나타냅니다.
- db=∂b∂J(w,b) : 함수의 기울기가 b 방향으로 얼만큼 변했는지 나타냅니다.
- 계산 그래프로 미분하기
- - 미분의 연쇄법칙이란 합성함수의 도함수에 대한 공식입니다. 합성함수의 도함수는 합성함수를 구성하는 함수의 미분을 곱함으로써 구할 수 있습니다.
- 입력변수 a 를 통해서 출력변수 J 까지 도달 하기 위해서 a→v→J 의 프로세스로 진행됩니다. 즉, 변수 a 만 보게 된다면, J = J(u(a)) 라는 함성함수가 될것 입니다.
- 강의에서 합성함수를 a로 미분한 값 d ad J 를 구하기 위해서 dvdJ 와 dadv 의 곱으로 표현 했습니다. 이러한 법칙이 연쇄법칙입니다.
- - 코드 작성시 편의를 위해서 표기법을 아래와 같이 정의합니다.
- 최종변수를 Final output var, 미분하려고 하는 변수를 var 라고 정의 한다면
- d vard Final output var=d var
- 로지스틱 회귀의 경사하강법과 m개 샘플의 경사하강법
- da=−ay+1−a1−y
- dz = a - y
- dw1=dw1dL=x1dz
- db=dbdL=dz
- - 로지스틱 회귀에서 비용 함수는 다음과 같이 표현할 수 있습니다.
J(w,b)=m1∑i=1i=m(L(a(i),y(i)))
이를 코드로 표현하면 다음과 같다.

- 현재 코드에서는 특성의 개수를 2개로 가정하였지만, 만약 특성의 개수가 많아진다면 이 또한 for문을 이용해 처리해야 합니다. 즉, 이중 for문을 사용하게 되며 이로인해 계산속도가 느려지게 됩니다.
- 다음 시간에는 vectorization을 통해 for문을 사용하지 않고 처리할 수 있는 방법을 배우겠습니다.
'코딩로그 > Andrew Ng's ML class' 카테고리의 다른 글
| 신경망과 딥러닝 - 심층 신경망 네트워크 (0) | 2019.12.24 |
|---|---|
| 신경망과 딥러닝 - 얕은 신경망 네트워크 (0) | 2019.12.24 |
| 신경망과 딥러닝 - 파이썬과 벡터화 (0) | 2019.12.24 |
| Numpy 기초, 기본 정리 (0) | 2019.12.05 |



